¿Cuánto es x por x? Explicación y ejemplos fáciles
Al multiplicar x por x se obtiene x2.
x2 se lee como “x elevado al cuadrado” o simplemente “x al cuadrado”.
¿Por qué x por x es x2?
El resultado de x por x es x2.
Se trata de un resultado muy fácil de verificar, gracias a la propiedad de la multiplicación de potencias de igual base.
En álgebra se utiliza la letra X como una forma de llamar a una cantidad que toma valores desconocidos, aunque pueden utilizarse también otras letras.
La propiedad de la multiplicación de potencias de igual base afirma que “al multiplicar dos bases idénticas, se escribe la misma base y se suman los exponentes“.
xa∙xb = xa+b
El exponente igual a 1 de la x suele omitirse, de manera que x1 = x.
Si queremos saber cuánto es x por x:
La base es x (se escribe la misma) y se suman los exponentes a+b (sus valores son iguales a 1):
x∙x = x1+1 = x2
Ejemplos de la propiedad de la multiplicación de potencias de igual base
Veamos algunos ejemplos numéricos muy simples:
2×2 = 22 = 4
3×3 = 32 = 9
4×4 = 42 = 16
(−2) × (−2) = 22 = 4
Nótese que el signo negativo antepuesto no cambia el resultado, ya que de acuerdo a la ley de los signos, al multiplicar dos cantidades negativas se obtiene resultado positivo.
En los ejemplos anteriores se utilizaron números enteros, pero la operación es igualmente válida para números decimales, fraccionarios, reales y complejos.
El área de un cuadrado
El cuadrado de un número aparece con frecuencia en el cálculo de áreas de figuras geométricas regulares. Por ejemplo, la del cuadrado, que es un polígono sencillo de cuatro lados, todos los cuales tienen la misma medida.
El área de un cuadrado viene dada por el cuadrado de su lado, si a este se lo llama “x”, entonces el área A del cuadrado vale x2.
Ejemplo del área de un cuadrado
El área A de cuadrado cuyo lado es x = 5 unidades es igual a:
A = 52 = 5×5 = 25 unidades de área
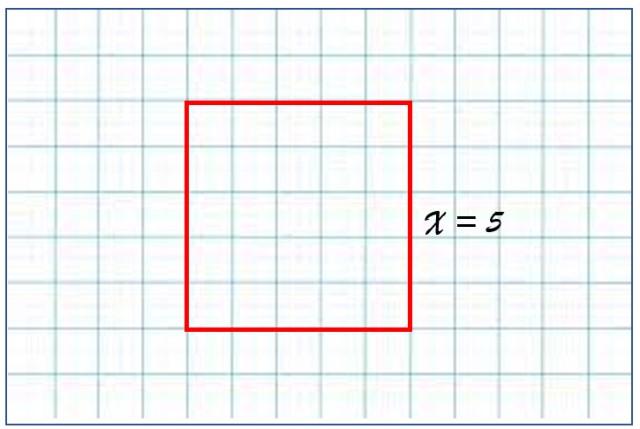
Este resultado tiene sentido, ya que el cuadrado consta de 5 filas y 5 columnas de cuadrados más pequeños, de lado igual a 1. Si el lector observa con atención la figura, se dará cuenta de que el cuadrado rojo consta de 25 pequeños cuadrados de área unitaria.
Importante:
Las unidades en este ejemplo son arbitrarias, pueden ser metros, centímetros, pulgadas u otras. Aquí no se especificaron, pero en cualquier caso, el área respectiva vendría dada en metros al cuadrado, centímetros al cuadrado, pulgadas al cuadrado u otras. El área siempre viene dada en unidades de longitud al cuadrado.
El cuadrado de números fraccionarios y decimales
Para hallar el cuadrado de un número fraccionario, que es aquel que consiste de un numerado y un denominador, separados por la línea de fracción, es necesario multiplicar consigo mismo el numerador, así como el denominador, obteniéndose un nuevo número fraccionario.
Ejemplos de cuadrados de números fraccionarios
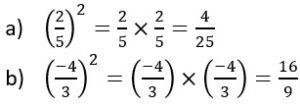
Ejemplos de cuadrados de números decimales
En cuanto al cuadrado de un número decimal, hay que seguir las reglas de la multiplicación para números decimales.
a) 0.62 = 0.6 × 0.6 = 0.36
b) (−0.4)2 = (−0.4)× (−0.4) = 0.16
Tanto en este ejemplo como el correspondiente de la sección anterior, se observa que el cuadrado de un número negativo siempre es positivo. Esto es cierto para las potencias pares, no solo para el cuadrado.
