Derivadas sucesivas: definición, ejemplos y ejercicios resueltos

¿Qué son las derivadas sucesivas?

Las derivadas sucesivas son las derivadas de una función después de la segunda derivada. El proceso para calcular las derivadas sucesivas es el siguiente: se tiene una función f, la cual podemos derivar y obtener así la función derivada f’. A dicha derivada de f podemos volver a derivarla, obteniendo (f’)’.

Esta nueva función se denomina segunda derivada; todas las derivadas calculadas a partir de la segunda son sucesivas; estas, llamadas también de orden superior, poseen grandes aplicaciones, como dar información sobre el trazo de la gráfica de una función, la prueba de la segunda derivada para extremos relativos y la determinación de series infinitas.

Definición

Usando la notación de Leibniz, tenemos que la derivada de una función “y” con respecto a “x” es dy/dx. Para expresar a la segunda derivada de “y” usando la notación de Leibniz, escribimos de la siguiente manera:

En general, podemos expresar las derivadas sucesivas como sigue con la notación de Leibniz, donde n representa al orden de la derivada.

Otras notaciones usadas son las siguientes:

Algunos ejemplos en donde podemos ver las diferentes notaciones son:

Ejemplo 1

Obtener todas las derivadas de la función f definida por:

Usando las técnicas de derivación usuales, tenemos que la derivada de f es:

Repitiendo el proceso podemos obtener la segunda derivada, la tercera derivada y así sucesivamente.

Nótese que la cuarta derivada es cero y la derivada de cero es cero, por lo cual tenemos que:

Ejemplo 2

Calcular la cuarta derivada de la siguiente función:

Derivando la función dada tenemos como resultado:

Velocidad y aceleración

Una de las motivaciones que llevaron al descubrimiento de la derivada fue la búsqueda de la definición de la velocidad instantánea. La definición formal es la siguiente:

Sea y = f(t) una función cuya gráfica describe la trayectoria de una partícula en un instante t, entonces su velocidad en un instante t viene dada por:

Una vez obtenida la velocidad de una partícula, podemos calcular aceleración instantánea, la cual está definida de la siguiente manera:

La aceleración instantánea de una partícula cuya trayectoria viene dada por y = f(t) es:

Ejemplo 1

Una partícula se mueve sobre una recta según la función posición:

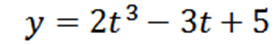
Donde “y” se mide en metros y “t” en segundos.

• ¿En qué instante su velocidad es 0?
• ¿En qué instante su aceleración es 0?

Al derivar la función posición “y” tenemos que su velocidad y aceleración vienen dadas respectivamente por:

Para poder responder la primera pregunta, basta con determinar cuándo se hace cero la función v; esto es:

Procedemos con la siguiente pregunta de manera análoga:

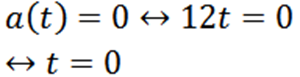
Ejemplo 2

Una partícula se desplaza sobre una recta de acuerdo con la siguiente ecuación de movimiento:

Determinar “t, y” y “v” cuando a = 0.

Sabiendo que la velocidad y la aceleración vienen dadas por

Procedemos a derivar y obtenemos:

Haciendo a = 0, tenemos:

De donde podemos deducir que el valor de t para que a sea igual a cero es de t = 1.

Luego, evaluando en t = 1 la función posición y la función velocidad, tenemos que:

Aplicaciones

Derivación mplícita

Las derivadas sucesivas también se pueden obtener por derivación implícita.

Ejemplo

Dado la siguiente elipse, encontrar “y”:

Derivando implícitamente con respecto a x, tenemos:

Luego, volviendo a derivar implícitamente con respecto a x, nos da:

Finalmente, tenemos:

Extremos relativos

Otro uso que podemos darle a las derivadas de segundo orden es en el cálculo de extremos relativos de una función.

El criterio de la primera derivada para extremos locales nos dice que si tenemos una función f continua en un intervalo (a, b) y existe un c que pertenece a dicho intervalo tal que f´se anula en c (es decir, que c es un punto crítico), puede ocurrir uno de estos tres casos:

• Si f´(x) > 0 para cualquier x perteneciente a (a,c) y f´(x)0 para x perteneciente a (c,b), entonces f(c) es un máximo local.
• Si f´(x) 0 para cualquier x perteneciente a (a,c) y f´(x)>0 para x perteneciente a (c,b), entonces f(c) es un mínimo local.
• Si f´(x) tiene igual signo en (a,c) y en (c,b), implica que f(c) no es un extremo local.

Usando el criterio de la segunda derivada podemos saber si un número crítico de una función es un máximo o un mínimo local, sin tener que ver cuál es el signo de la función en los intervalos antes mencionados.

El criterio de la segunda deriva nos dice que si f´(c) = 0 y que f´´(x) es continua en (a, b), ocurre que si f´´(c) > 0 entonces f(c) es un mínimo local y si f´´(c) 0 entonces f(c) es un máximo local.

Si f´´(c) = 0, no podemos concluir nada.

Ejemplo

Dada la función f(x)= x⁴ + (4/3)x³ – 4x², encontrar los máximos y mínimos relativos de f aplicando el criterio de la segunda derivada.

Primero calculamos f´(x) y f´´(x) y tenemos:

f´(x) = 4x³ + 4x² – 8x

f´´(x) = 12x² + 8x – 8

Ahora, f´(x) = 0 si, y solo si 4x(x + 2)(x – 1)= 0, y esto ocurre cuando x=0, x=1 o x=– 2.

Para determinar si los números críticos obtenidos son extremos relativos basta con evaluar en f´´ y así observar su signo.

f´´(0) = – 8, por lo que f(0) es un máximo local.

f´´(1) = 12, por lo que f(1) es un mínimo local.

f´´(– 2) = 24, por lo que f(– 2) es un mínimo local.

Serie de Taylor

Sea f una función definida como sigue:

Esta función posee un radio de convergencia R > 0 y tiene derivadas de todos los órdenes en (-R, R). Las derivadas sucesivas de f nos dan:

Tomando x = 0, podemos obtener los valores de c_n en función de sus derivadas como sigue:

Si tomamos a n = 0 como la función f (es decir, f^0=f), entonces podemos reescribir la funcion como sigue:

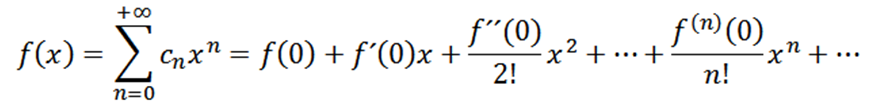
Ahora consideremos la función como una serie de potencias en x = a:

Si realizamos un análisis análogo al anterior, tendríamos que podemos escribir la función f como:

Estas series se conocen como series de Taylor de f en a. Cuando a = 0 tenemos el caso particular que se llama serie de Maclaurin. Este tipo de series es de gran importancia matemática sobre todo en el análisis numérico, ya que gracias a estas podemos definir funciones en las computadoras tales como e^x , sen(x) y cos(x).

Ejemplo

Obtener la serie de Maclaurin para e^x.

Nótese que si f(x)= e^x, entonces f⁽ⁿ⁾(x)= e^x y f⁽ⁿ⁾(0) = 1, por lo cual su serie de Maclaurin es: