¿Cuántos diámetros tiene una circunferencia?
Una circunferencia tiene infinitos diámetros. Es fácil ver que es así, si se parte de la definición de diámetro, que es el segmento que pasa simultáneamente por el centro de la circunferencia y por dos puntos de la misma.
En la siguiente figura, a la izquierda, se observa la línea amarilla correspondiente a un diámetro de la circunferencia y la divide en dos partes. En el lado derecho se dibujaron otros tres diámetros en distintos colores: azul, verde y rosa. Todos tienen la misma longitud y satisfacen la condición de unir dos puntos de la circunferencia, pasando por el centro de la misma.
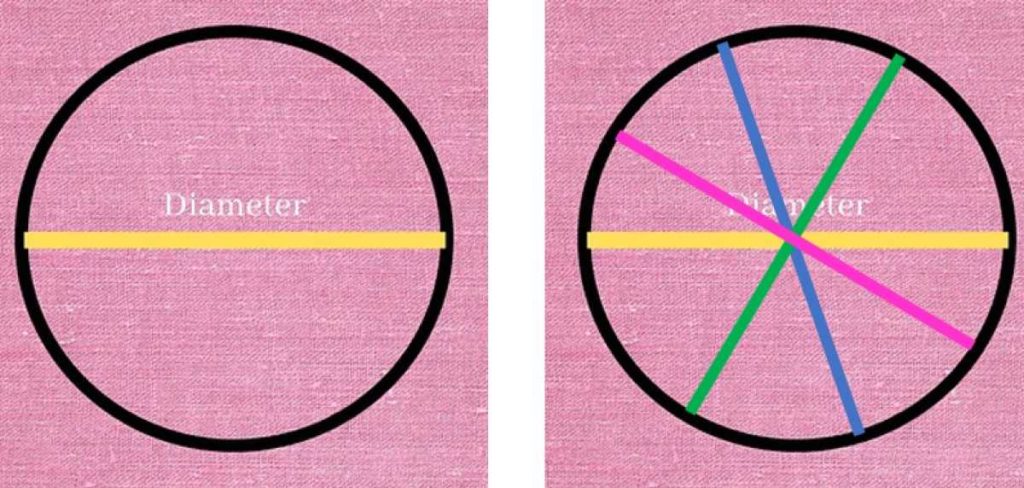
Como se puede ver, las posibilidades para trazar diámetros son infinitas, pues infinitos son los puntos que forman la circunferencia. Lo mismo puede afirmarse acerca del radio, que es el segmento que une un punto cualquiera de la circunferencia con el centro: se puede trazar un número infinito de radios.
Y al colocar dos radios opuestos uno del otro, se obtiene un diámetro, pues el radio mide la mitad de este.
Diámetro, radio y longitud de la circunferencia
Sea D el diámetro de una circunferencia cualquiera y R, su radio. Como el diámetro mide el doble que el radio, se puede escribir:
D = 2∙R
Significa que, si el radio de una circunferencia es, por ejemplo, R = 5 cm, el diámetro de la misma es D = 2∙5 cm = 10 cm.
Al diámetro también se le conoce como la cuerda mayor. Las cuerdas son líneas o segmentos que se trazan entre dos puntos cualesquiera de la circunferencia, pero que no necesariamente pasan por el centro. Solo el diámetro tiene esa distinción.
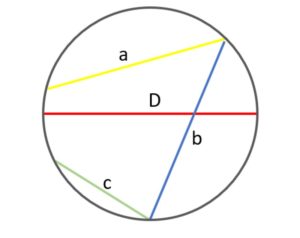
En la siguiente figura se puede apreciar la diferencia y ver por qué, en efecto, el diámetro (rojo) es la mayor de las cuerdas que se pueden dibujar sobre la circunferencia:
Eso sí, la medida del diámetro (y por consiguiente la del radio) es la misma en una circunferencia dada. Al variar, se obtiene una circunferencia más pequeña o o más grande, según.
En cambio, el tamaño de las cuerdas de una misma circunferencia varia, según lo lejos o cerca que estén los puntos que se unen. En el ejemplo mostrado, la cuerda “c” de color verde es ostensiblemente más corta que las cuerdas “a” y “b”.
Y el número de cuerdas que se pueden trazar también es infinito.
El perímetro de la circunferencia
Por su parte, la longitud de la circunferencia equivale a su perímetro o contorno. Tiene relación con su diámetro, puesto que cuanto mayor sea este, más grande es la circunferencia (su perímetro es mayor).
La razón o cociente entre perímetro y diámetro es una constante llamada π (se lee “pi”). El valor de π es 3.141592… Los puntos suspensivos indican que la cantidad de decimales e infinita, lo cual se debe a que pi es un número irracional. Sin embargo, a efectos prácticos, pi se puede redondear simplemente a 3.14
Si el perímetro se denota como C y el diámetro como D, esta razón se plantea del siguiente modo:
C / D = π
Por lo tanto, la fórmula para la longitud de la circunferencia es:
C = π∙D
O si se prefiere en función del radio R:
C = 2π∙R
Ejemplo ilustrativo
En la imagen se muestran tres circunferencias idénticas, designadas con las letras A, B y C. En cada una, la hormiga recorre el camino sobre los segmentos del color azul, para ir desde un punto a otro de la circunferencia.
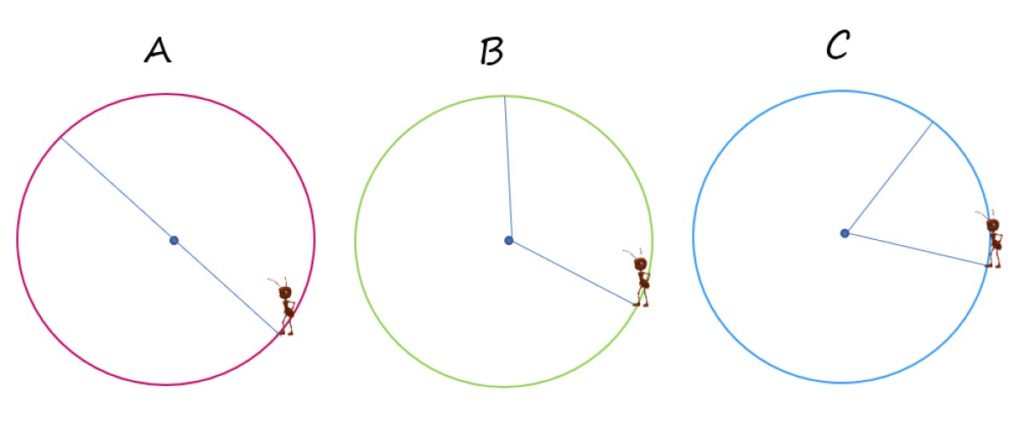
1.- ¿En cuál de los casos el desplazamiento ocurre exactamente sobre el diámetro de la circunferencia?
Respuesta
Solamente en el caso A, pues ese camino pasa por el centro de la circunferencia y va desde un punto a otro de la misma.
2.- ¿Cuántos radios recorre el insecto en cada caso?
Respuesta
En cualquiera de los tres casos la hormiga recorre dos radios de la circunferencia.
3.- ¿Cuál de los trayectos corresponde a la mayor distancia?
Respuesta
El trayecto es igual de largo en cada caso, equivalente a dos radios de la circunferencia.
4.- ¿En qué caso la hormiga queda más alejada de su punto de partida?
Respuesta
En el caso A, ya que queda en el punto que está justamente enfrente de ella, en los restantes, la hormiga queda más cerca del punto de partida.
5.- ¿Y en qué caso la hormiga finaliza el recorrido quedando más cerca de su punto de origen?
Respuesta
En el caso C.
6.- Si el radio de las circunferencias es 20 cm, ¿cuántos centímetros mide cada trayecto?
Respuesta
Ya que la hormiga recorre una distancia igual a dos radios, la distancia total recorrida es de 40 cm.
Ejercicios resueltos
Ejercicio 1
Calcular el radio de una circunferencia cuyo diámetro es de 4.5 m.
Solución
El radio es la mitad del diámetro, si este mide 4.5 cm, entonces el radio R es de 2.25 cm.
Ejercicio 2
Hallar el perímetro de la circunferencia del ejercicio 1.
Solución
El perímetro se calcula a través del diámetro o a través del radio, como se prefiera. En el primer caso:
C = π∙D
Suponiendo que π = 3.14 para redondear, la sustitución de valores da el siguiente resultado:
C = π∙D = 3.14 ∙ 4.5 cm = 14.13 cm
Ejercicio 3
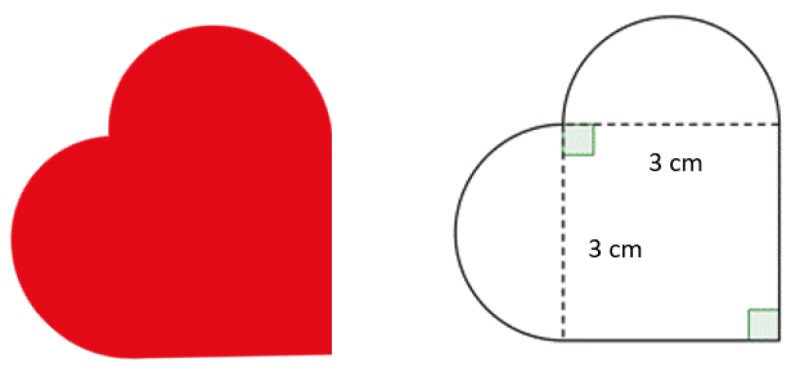
Se le pide a un diseñador que dibuje un logo en forma de corazón, con las dimensiones indicadas en la figura. Las partes curvadas corresponden a semicircunferencias exactas.
Con esta información responder:
- ¿Cuál es el radio de las semi-circunferencias?
- ¿Cuánto mide el perímetro del corazón?
Solución a
El diámetro de las semicircunferencias equivale al lado del cuadrado, que es 3 cm. Por lo tanto, su radio, que es la mitad, mide 1.5 cm.
Solución b
El perímetro de la figura en forma de corazón es la suma de los dos lados exteriores del cuadrado y el perímetro de las semicircunferencias. Como son idénticas, su perímetro equivale al de una circunferencia completa de diámetro 3 cm:
C = π∙D = 3.14 ∙ 3 cm = 9.42 cm
Por lo tanto, el perímetro P de la figura es:
P = 9.42 cm + 3 cm + 3 cm = 15.42 cm
