Congruencia: figuras congruentes, criterios, ejemplos, ejercicios
La congruencia, en geometría, señala que si dos figuras planas tienen igual forma y dimensiones, estas son congruentes. Por ejemplo, dos segmentos son congruentes cuando sus longitudes son iguales. Asimismo los ángulos congruentes tienen la misma medida, aunque no estén orientados de la misma manera en el plano.
El término “congruencia” proviene del latín congruentia, cuyo significado es correspondencia. Así pues, dos figuras congruentes se corresponden exactamente la una con la otra.
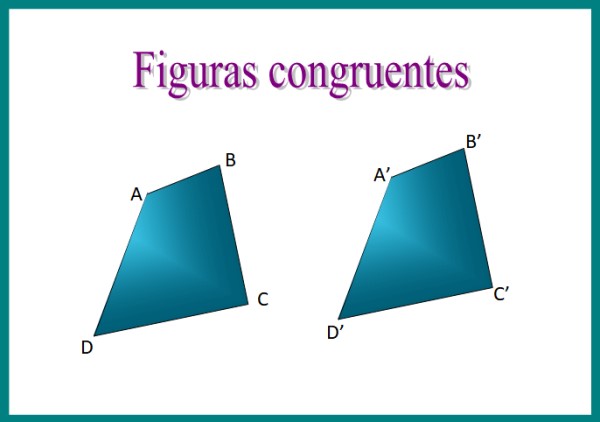
Por ejemplo, si superponemos los dos cuadriláteros de la imagen, encontraremos que son congruentes, ya que la disposición de sus lados es idéntica y estos miden lo mismo.
Al colocar los cuadriláteros ABCD y A’B’C’D’ uno sobre el otro, las figuras coincidirán exactamente. Los lados coincidentes se llaman lados homólogos o correspondientes y para expresar congruencia se utiliza el símbolo ≡. Entonces podemos afirmar que ABCD ≡ A’B’C’D’.
Índice del artículo
Las siguientes características son comunes a los polígonos congruentes:
-Igual forma y tamaño.
-Idénticas medidas de sus ángulos.
-Las misma medida en cada uno de sus lados.
En el caso de que dos polígonos en cuestión sean regulares, es decir, que todos los lados y los ángulos internos midan lo mismo, la congruencia queda asegurada cuando se cumple alguna de las siguientes condiciones:
-Los lados son congruentes
-Las apotemas tienen la misma medida
-El radio de cada polígono mide igual
La apotema de un polígono regular es la distancia entre el centro y uno de los lados, mientras que el radio corresponde a la distancia entre el centro y un vértice o esquina de la figura.
Los criterios de congruencia se utilizan con frecuencia porque muchísimas partes y piezas de todo tipo se fabrican en serie y deben tener la misma forma y medidas. De esta manera pueden reemplazarse fácilmente cuando sea necesario, por ejemplo tuercas, tornillos, láminas o los adoquines del suelo en la calle.

Existen conceptos geométricos relacionados con la congruencia, por ejemplo las figuras idénticas y las figuras semejantes, que no necesariamente implican que las figuras sean congruentes.
Obsérvese que las figuras congruentes son idénticas, sin embargo los cuadriláteros de la figura 1 podrían orientarse de maneras distintas sobre el plano y aun así seguir siendo congruentes, ya que la orientación distinta no cambia el tamaño de sus lados ni el de sus ángulos. En tal caso dejarían de ser idénticos.
El otro concepto es el de la semejanza de figuras: dos figuras planas son semejantes si tienen la misma forma y sus ángulos internos miden lo mismo, aunque el tamaño de las figuras puede ser diferente. Si este es el caso, las figuras no son congruentes.
Tal como indicamos al comienzo, los ángulos congruentes tienen la misma medida. Hay varias maneras de obtener ángulos congruentes:
Ejemplo 1
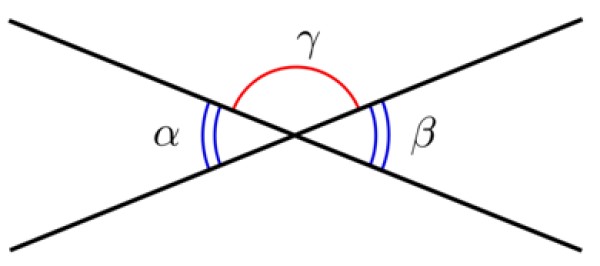
Dos rectas con un punto en común definen dos ángulos, llamados ángulos opuestos por el vértice. Estos ángulos tienen la misma medida, por lo tanto son congruentes.
Ejemplo 2
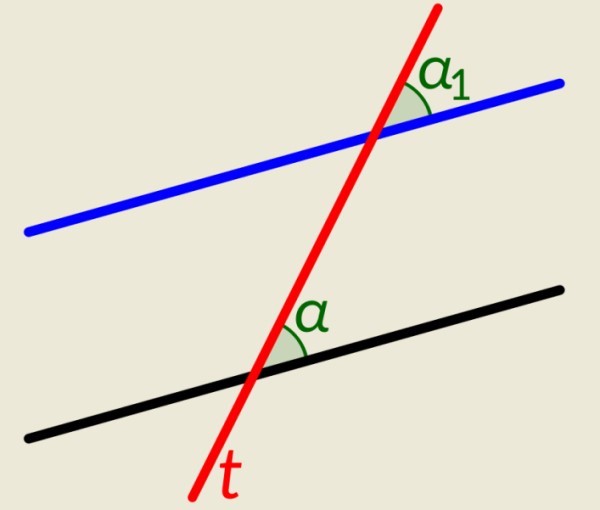
Se tienen dos rectas paralelas más una recta t que las intersecta a ambas. Al igual que en el ejemplo anterior, cuando esta recta intersecta a las paralelas genera ángulos congruentes, uno en cada recta al lado derecho y otros dos en el lado izquierdo. En la figura se muestran α y α1, a la derecha de la recta t, que son congruentes.
Ejemplo 3
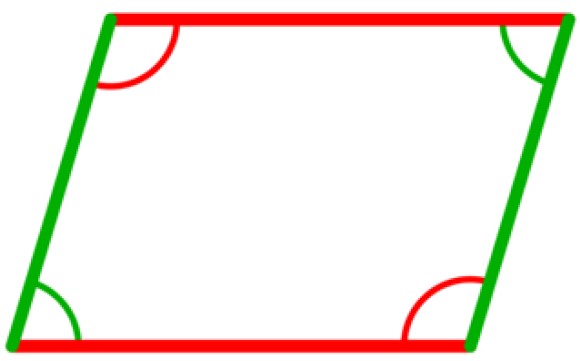
En un paralelogramo hay cuatro ángulos internos, los cuales son congruentes dos a dos. Son los que están entre vértices opuestos, como se muestra en la siguiente figura, en la cual los dos ángulos en verde son congruentes, así como los dos ángulos en rojo.
Dos triángulos de idéntica forma e igual tamaño son congruentes. Para verificar esto hay tres criterios que se pueden examinar en búsqueda de la congruencia:
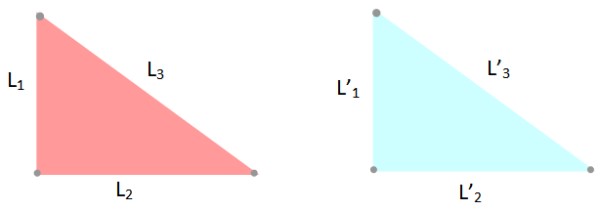
–Criterio LLL: los tres lados de los triángulos tienen las mismas medidas, por lo tanto L1 =L’1; L2 =L’2 y L3 =L’3.
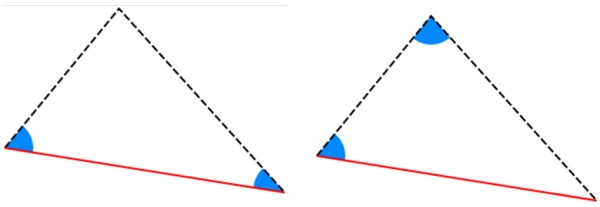
–Criterios ALA y AAL: los triángulos tienen dos ángulos internos iguales y el lado entre dichos ángulos tiene la misma medida.
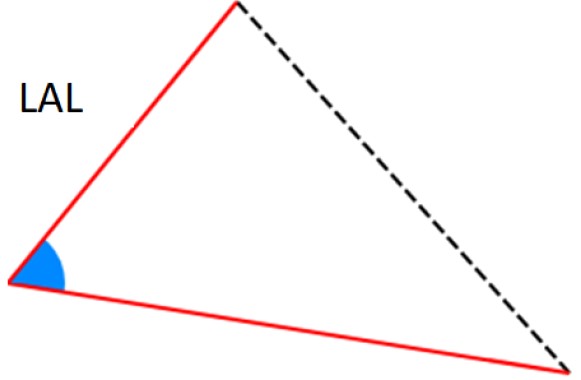
–Criterio LAL: dos de los lados son idénticos (correspondientes) y entre ellos hay un mismo ángulo.
En la siguiente figura se muestran dos triángulos: ΔABC y ΔECF. Se sabe que AC=EF, que AB = 6 y que CF = 10. Además los ángulos ∡BAC y ∡FEC son congruentes y los ángulos ∡ACB y ∡FCB también lo son.
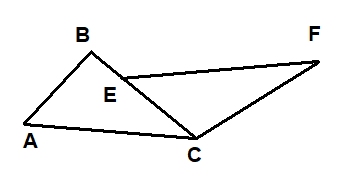
Entonces la longitud del segmento BE es igual a:
(i) 5
(ii) 3
(iii) 4
(iv) 2
(v) 6
Solución
Como los dos triángulos tienen un lado de igual longitud AC=EF comprendido entre los ángulos iguales ∡BAC = ∡CEF y ∡BCA = ∡CFE puede decirse que los dos triángulos son congruentes por el criterio ALA.
Es decir ΔBAC ≡ ΔCEF, por lo que se tiene que:
BA = CE = AB = 6
BC = CF = 10
AC = EF
Pero el segmento que quiere calcularse es BE = BC – EC = 10 – 6 = 4.
De modo que la respuesta correcta es la (iii).
En la figura que sigue se muestran tres triángulos. Se sabe además que los dos ángulos indicados miden 80º cada uno y que los segmentos AB = PD y AP = CD. Encontrar el valor del ángulo X señalado en la figura.
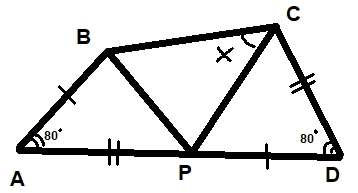
Solución
Hay que aplicar las propiedades de los triángulos, que se van detallando paso a paso.
Paso 1
Comenzando con el criterio de congruencia de triángulos LAL, puede afirmarse que los triángulos BAP y PDC son congruentes:
ΔBAP ≡ ΔPDC
Paso 2
Lo anterior conduce a afirmar que BP = PC, por lo tanto el triángulo ΔBPC es isósceles y ∡PCB = ∡PBC = X.
Paso 3
Si llamamos γ al ángulo BPC, se sigue que:
2x + γ = 180º
Paso 4
Y si llamamos β a los ángulos APB y DCP y α a los ángulos ABP y DPC se tiene que:
α + β + γ = 180º (ya que APB es un ángulo plano).
Paso 5
Además, α + β + 80º = 180º por suma de ángulos internos del triángulo APB.
Paso 6
Combinando todas estas expresiones se tiene que:
α + β = 100º
Paso 7
Y por lo tanto:
γ = 80º.
Paso 8
Finalmente se sigue que:
2X + 80º = 180º
Con X = 50º.
- Baldor, A. 1973.Geometría plana y del espacio. Cultural Centroamericana.
- CK-12 Foundation. Congruent Polygons. Recuperado de: ck 12.org.
- Disfruta las Matemáticas. Definiciones: Radio (polígono). Recuperado de: disfrutalasmatematicas.com.
- Math Open Reference. Testing Polygons for congruence. Recuperado de: mathopenref.com.
- Wikipedia. Congruencia (geometría). Recuperado de: es.wikipedia.org.
- Zapata, F. Triángulos, historia, elementos, clasificación, propiedades. Recuperado de: lifeder.com.
